Why the proof of closure under addition in Linear Map is $(T+S)(u+v)$ instead of $(T+S)(u)$ and $(T)(u+v)$? - Mathematics Stack Exchange

I am reading Linear Algebra Done Right and want to prove that $L(V, W)$ is a vector space. I have read the solution here: Why the proof of closure under addition in Linear Map is $(T+S)(u+v)$ inst

Solved Let T: R^2 rightarrow R^2 be a linear transformation

Solved (15 points) True or False. There is no partial

INTERSECTION COHOMOLOGY OF RANK 2 CHARACTER VARIETIES OF SURFACE

Lorentz transformation - Wikipedia

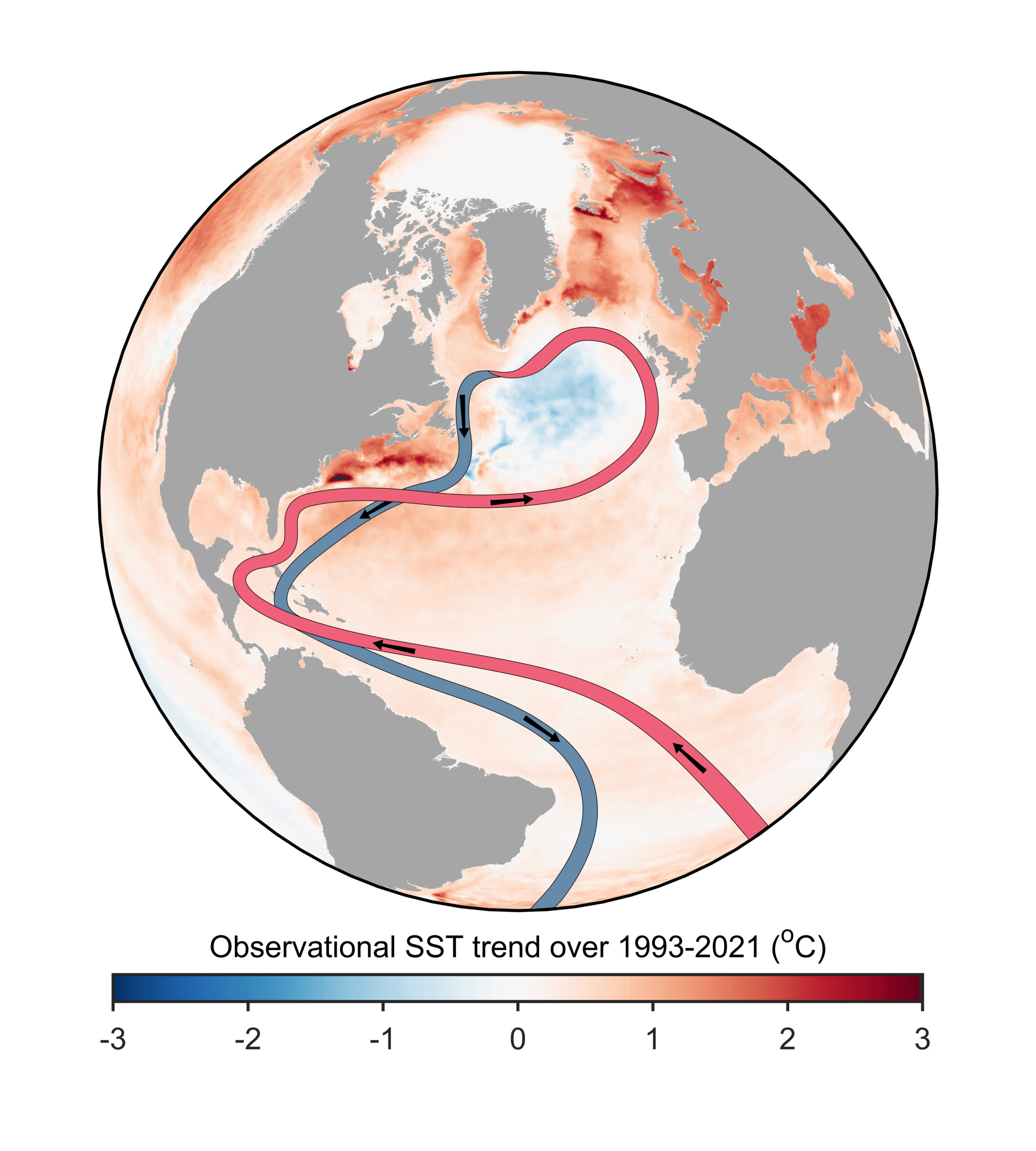
RealClimate: What is happening in the Atlantic Ocean to the AMOC?

Set closed under addition, Basic Linear Algebra

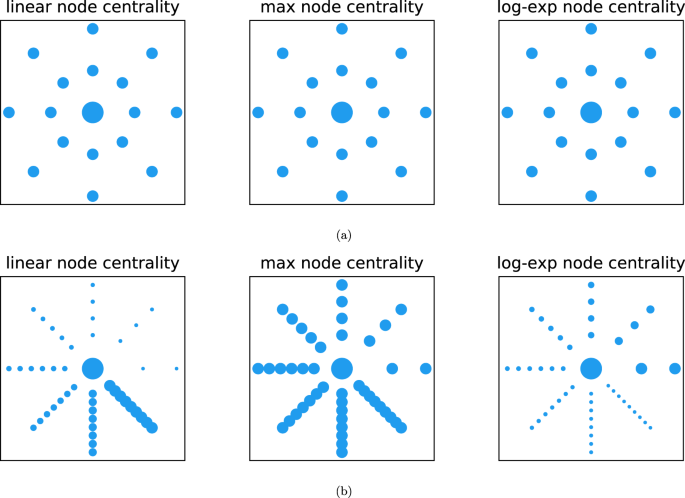
Node and edge nonlinear eigenvector centrality for hypergraphs

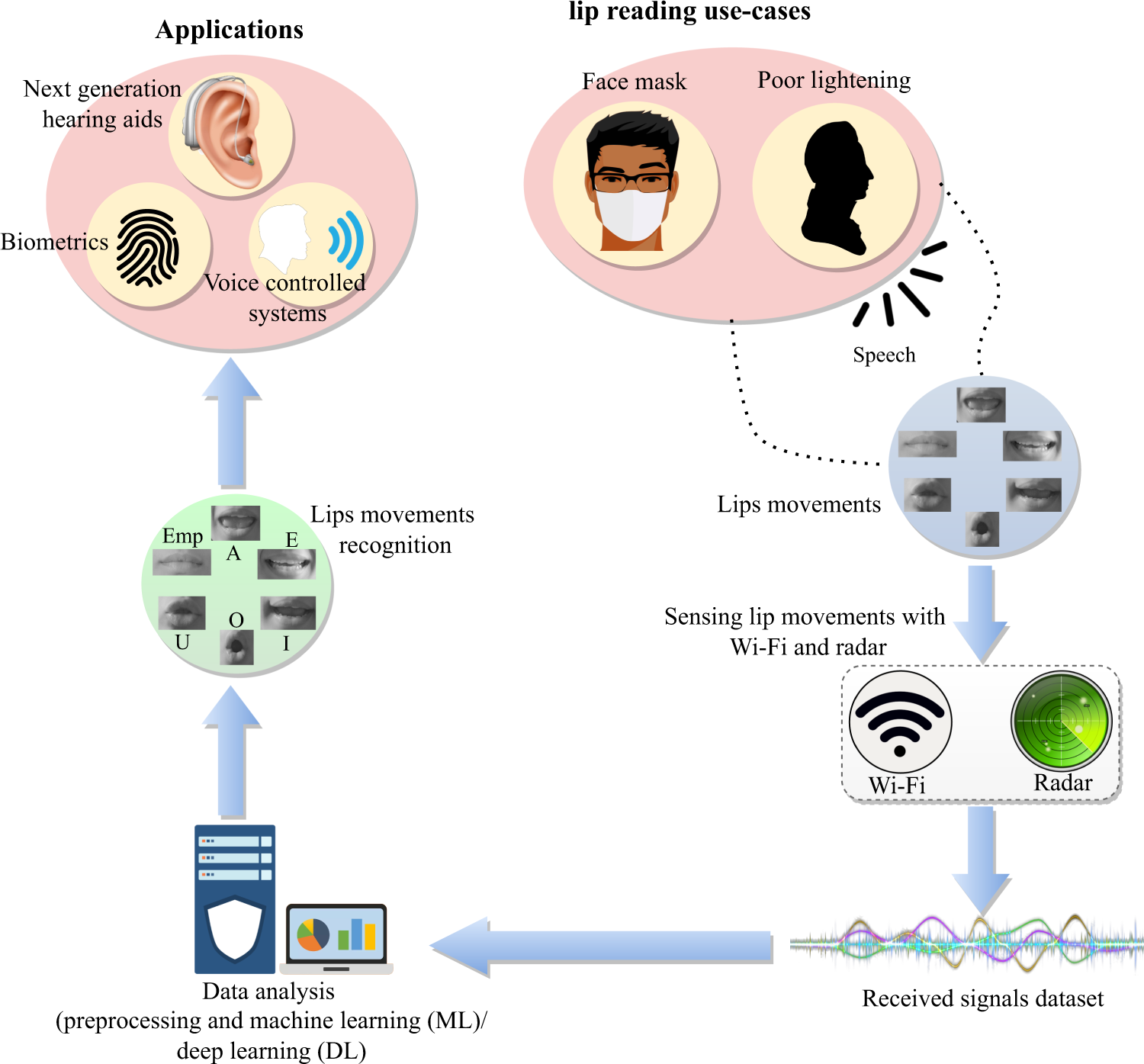
Pushing the limits of remote RF sensing by reading lips under the face mask

Solved (1 pt) Let T : R2 R2 be a linear transformation that