probability - Proof explanation - weak law of large numbers - Mathematics Stack Exchange

Let $(X_i)$ be i.i.d. random variables with mean $\mu$ and finite variance. Then $$\dfrac{X_1 + \dots + X_n}{n} \to \mu \text{ weakly }$$ I have the proof here: What I don't understand is, why it

probability theory - Showing that a sequence of random variables has CLP. - Mathematics Stack Exchange

Mathematics, Free Full-Text

fourier analysis - Proving Weierstrass' Approximation Theorem

The Law of Large Numbers - by Tivadar Danka

In computer science, is it possible to visually depict an infinite

Proof of the Law of Large Numbers Part 1: The Weak Law, by Andrew Rothman

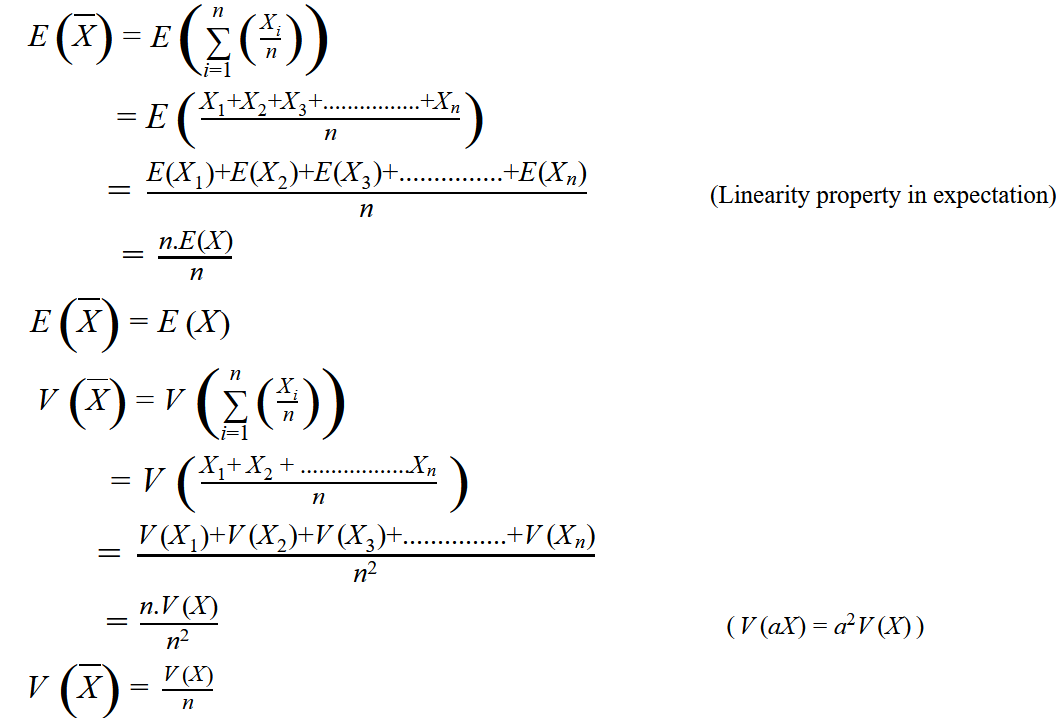
Laws of Large Numbers (detailed explanation), by Anirudh G

Proof of the Law of Large Numbers Part 2: The Strong Law, by Andrew Rothman

Law of Large Numbers Strong and weak, with proofs and exercises

probability - Question about convergence of a series - need help understanding a proof for the strong law of large numbers - Mathematics Stack Exchange

Law of large numbers - Wikipedia